02. Reconstruction I

This tutorial demonstrates the reconstruction of a measurement obtained in computerized tomography. As mathematical construct the radon transform is obtained. The implementation of the Astra-Toolbox is used.

We create a scenario with a 180 equal distributed angles.

import numpy as np
import matplotlib.pyplot as plt

from recon.utils import psnr
from recon.operator.ct_radon import CtRt
from recon.interfaces import Recon, Smoothing

from matplotlib import image

# load image as pixel array
gt = image.imread("../data/phantom.png")
gt = gt/np.max(gt)

ntheta = 180
theta = np.linspace(0, 180, ntheta, endpoint=False)
sigma = 0.01
R = CtRt(gt.shape, center=[gt.shape[0]//2, gt.shape[1]//2], theta=theta)

y = R*gt.ravel()
y_max = np.max(y)

n = np.random.normal(0, sigma*y_max, size=y.shape)
y = y + n

x_rec = np.reshape(R.inv*y.ravel(), gt.shape)

fig, axs = plt.subplots(1, 3, figsize=(14, 5))
axs[0].imshow(gt, vmin=0, vmax=1)
axs[0].set_title('Model')
axs[0].axis('tight')
axs[1].imshow(np.reshape(y, R.image_dim).T)
axs[1].set_title('Data')
axs[1].axis('tight')
axs[2].imshow(x_rec, vmin=0, vmax=1)
axs[2].set_title("FBP - PSNR: "+str(psnr(gt, x_rec)))
axs[2].axis('tight')
fig.tight_layout()
plt.show(block=False)

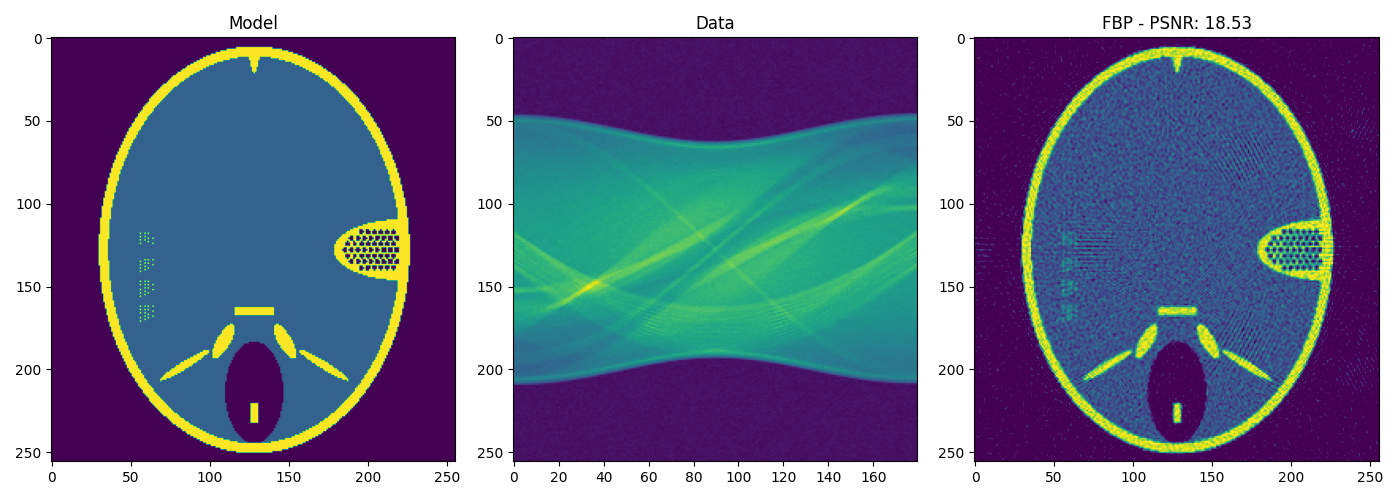
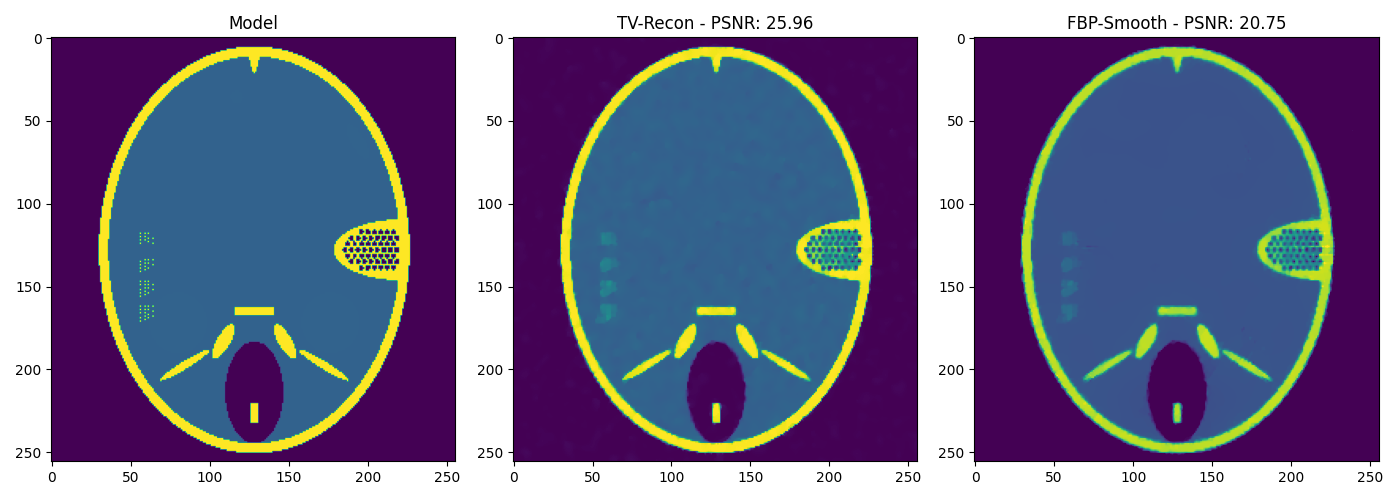
Now we solve the problem using the optimization problem. A comparison to the denoising of the FBP solution is shown.

lam = 15
rec = Recon(operator=R, domain_shape=gt.shape, reg_mode='tv', alpha=1, lam=lam, extend_pdhgm=True)
x_tv = rec.solve(data=y.ravel(), max_iter=1000, tol=1e-4)

tv_smoothing = Smoothing(domain_shape=gt.shape, reg_mode='tv', lam=10, tau='calc')
fbp_smooth = tv_smoothing.solve(data=x_rec, max_iter=1000, tol=1e-4)


fig, axs = plt.subplots(1, 3, figsize=(14, 5))
axs[0].imshow(gt, vmin=0, vmax=1)
axs[0].set_title('Model')
axs[0].axis('tight')
axs[1].imshow(x_tv, vmin=0, vmax=1)
axs[1].set_title("TV-Recon - PSNR: "+str(psnr(gt, x_tv)))
axs[1].axis('tight')
axs[2].imshow(fbp_smooth, vmin=0, vmax=1)
axs[2].set_title("FBP-Smooth - PSNR: "+str(psnr(gt, fbp_smooth)))
axs[2].axis('tight')
fig.tight_layout()
plt.show(block=False)

Out:

/Users/lucasplagwitz/git_projects/recon/recon/solver/pd_hgm_extend.py:137: RuntimeWarning: divide by zero encountered in double_scalars
  self.sens = np.linalg.norm(p_gap)/np.linalg.norm(p_old)
inf
0.0575879430761
0.0250657895096
0.0123394724924
0.00698178486739
0.00383661007699
0.00223954403196
0.00136202788
0.000839463622562
0.000535423830805
0.000357559031815
0.000246971744871
0.000188842471093
0.000151375819315
0.000126698668617
0.000109222033788
9.76307796608e-05
 Early stopping.
 Early stopping.